组合数学¶

组合数学是一门古老而迷人的学科。传说早在

\texttt{114514}

年前，一位名为忆哀的神灵来到地球，发现了人类——另一种有智慧的物种。她觉得这很有趣，为了加速人类文明的发展，她向人间传下了一类计数问题——十二重计数，这也正是组合数学的开端。而只有搞明白这类问题，才能在组合数学上继续深入。

基础内容¶

四大原理¶

加法原理：分类相加，

N=\sum m_n

乘法原理：分步相乘，

N=\prod m_n

减法原理：正难则反，

|A|=|S|-|S\setminus A|,A\subseteq S

除法原理：反悔划分。

这玩意想不明白回初赛重造。

注：本文将会偶尔用到大型运算符，不清楚的见我数列进阶。

经典例题¶

从 $A\to B$ 有 $2$ 条路， $B\to D$ 有 $3$ 条路；
从 $A\to C$ 有 $4$ 条路， $C\to D$ 有 $5$ 条路。

问：从 $A\to D$ 一共有几条路？

解：

2\times3+4\times5=26

完毕！

经典应用：因数个数¶

例题， $2160$ 有多少个不同的正因数。

分解质因数，

\begin{aligned} 2160&=2\times5\times 216\\ &=2^4\times5\times 27\\ &=2^4\times3^3\times5 \end{aligned}

注意到每一个指数一次比他小的都是其因数，

因数个数，

(4+1)(3+1)(1+1)=40

In general:

N=p_1^{c_1}p_2^{c_2}\dots p_k^{c_k}

对于，

\forall p_i\in\mathbb P,p_i\neq p_j(i\neq j)

那么，任意，

M=p_1^{b_1}p_2^{b_2}\dots p_k^{b_k}

对于，

\forall b_i\le c_i

的 $M$ 都是 $N$ 的因数，因数个数为，

\mathit{cnt}=(c_1+1)(c_2+1)\dots(c_k+1)

经典应用：子集个数¶

对于集合，

A=\{1,2,3,\dots,10\}

其子集个数是多少？

对于每一个数，其要么出现在子集中，要么不出现，

因此，子集个数，

2^{10}

In general:

大小为 $N$ 的集合，其，

子集个数： $2^N$ ；

真子集个数： $2^N-1$ ；

非空子集个数： $2^N-1$ ；

非空真子集个数： $2^N-2$ 。

排列数和组合数¶

排列数¶

定义，排列数为 $A(n,m)$ 表示：

从 $n$ 个物品中，选出 $m$ 个进行排列的方案数。

也记为， $A\begin{smallmatrix}n\\m\end{smallmatrix}$ ，但是这样太麻烦了，我不喜欢（

早年时期也记为 $P(n,m)$ ，P 表示 Permutation（排列）。

定义式¶

按照定义，我们一次分析第 $i$ 个选哪个，

\def\arraystretch{1.2} \begin{array}{|c|c|}\hline \bm{i}&\small\texttt{方案数}\\\hline 1&n\\\hline 2&n-1\\\hline 3&n-2\\\hline \dots&\dots\\\hline m&n-m+1\\\hline \end{array}

因此，总方案数，

A(n,m)=n(n-1)(n-2)\dots(n-m+1)

这个是经典公式，即，

从 $n$ 开始，往下数 $m$ 个相乘。

我们知道阶乘的定义为，

x!=x(x-1)(x-2)\dots1

因此，类似的，

\boxed{A(n,m)={n!\over(n-m)!}}

由此，当 $m=n$ 时，

A(n,n)=n!=n(n-1)(n-2)\dots1

注意到其实后面的 $1$ 没啥用（

特殊的，我们定义，

0!=1

而一般默认 $A(n,m)$ 中 $n\ge m$ ，若大于了，规定为零。

至于为什么这么定义，从组合意义上是显然的，也可以参见下降幂。

组合数¶

定义，组合数为 $C(n,m)$ 表示：

从 $n$ 个物品中，选出 $m$ 个进行排列的方案数。

也记为 $C\begin{smallmatrix}n\\m\end{smallmatrix}$ ，C 表示 Combination（组合），学术上一般记为，

{n\choose m}

定义式¶

有些教材会先讲组合数，原因就是，

我们在排列中，从 $n$ 个物品中选择 $m$ 个进行排列，

这个本质其实是两个步骤，

从 $n$ 个物品中选择 $m$ 个，即 $C(n,m)$ ；
将这 $m$ 个进行排列，即 $A(m,m)=m!$ 。

因此，

A(n,m)=C(n,m)\times A(m,m)

\boxed{C(n,m)={A(n,m)\over A(m,m)}={n!\over(n-m)!m!}}

这个思路其实更加连贯。

拓展¶

有， $m!$ 整除任何连续的 $m$ 个整数的乘积。

证明，构造组合数。

一些性质¶

注意到组合数有更好的性质，所以下面主要是组合数的性质，

从定义可得，

\boxed{\tag1{n\choose m}={n\choose n-m}}

从 $n$ 个里面选 $m$ 个，等价于找出来 $n-m$ 个不选。

同样是定义得出，

\boxed{{n\choose m}={n\over m}{n-1\choose m-1}\tag{1 II}}

因此我们打了一个可爱的 Tag．

同样是定义得出，

\boxed{{n\choose m}{m\choose k}={n\choose k}{n-k\choose m-k}}\tag{1 III}

表示 $n$ 选 $m$ ， $m$ 选 $k$ 表示 $n$ 直接选 $k$ 然后再把 $m-k$ 补回去。

因此我们又打了一个可爱的 Tag．

经典递推式，

\boxed{\tag2{n\choose m}={n-1\choose m}+{n-1\choose m-1}}

相当于 $n$ 个选 $m$ 个，分讨其中一个选不选，可用于裂项。

另外有类比上面的，

\boxed{A_n^m=A_{n-1}^m+mA_{n-1}^{m-1}\tag{2 II}}

相当于 $n$ 个选 $m$ 个进行排列，分讨第 $n$ 个选不选。

下面是一些用到了大型运算符的性质，

\boxed{\sum_{i=0}^n{n\choose i}=2\tag3}

表示从 $n$ 个中，任意选 $0\sim n$ 个，自然就是 $2^n$ 种。

一个裂项的题。

\boxed{\sum_{i=m}^{2m}{i\choose m}={2m+1\choose m}\tag4}

考虑裂项，

{2m+1\choose m}={2m\choose m}+{2m\choose m-1}={2m\choose m}+{2m-1\choose m-1}+{2m-1\choose m-2}=\dots

用大型运算符表示，注意到选 $0$ 个可以随便换。

{2m+1\choose m}=\sum_{i=0}^{m-1}{2m-i\choose m-i}+{m+1\choose 0}=\sum_{i=0}^m{2m-i\choose m-i}

对里面的应用 $(1)$ ，得到，

{2m+1\choose m}=\sum_{i=0}^m{2m-i\choose m}=\sum_{0\le i\le m}{2m-i\choose m}

应用一些技巧（注意到 $2m-i$ 是的一个 Permutation），

{2m+1\choose m}=\sum_{0\le 2m-i\le m}{2m-(2m-i)\choose m}=\sum_{i=m}^{2m}{i\choose m}

Q.E.D.

同样的，两边乘上 $m!$ 就得到了排列的版本。

补充：解方程问题¶

解方程，

{n\choose a}={n\choose b}

首先，若，

a=b

那么是显然的，否则，应用性质 $(1)$ ，得，

a+b=n

自然也是显然的。

二项式定理¶

基本形式¶

\boxed{(a+b)^n=\sum_{i=0}^n{n\choose i}a^{n-i}b^n}

令 $b=1$ 可以得出最能体现性质的形式，

\boxed{(a+1)^n=\sum_{i=0}^n{n\choose i}a^n}

二项式定理也可以很容易扩展为多项式的形式：

\boxed{(x_1+\dots+x_k)^n=\sum_{n_1+\dots+n_k=n}{n\choose n_1,\dots,n_k}x_1^{n_1}\dots x_n^{n_k}}

有性质，

\boxed{\sum_{n_1+\dots+n_k=n}{n\choose n_1,\dots,n_k}=k^n}

问：下面这个有什么用？

答：可以用来检验你展开的对不对。

杨辉三角¶

递推式，

a_{i,1}=a_{i,i}=1\\ a_{i,j}=a_{i-1,j-1}+a_{i-1,j}

注意到形如组合数的形式，

\def\qq{\quad} \begin{array}{r|c} 1&1\\\hline 2&1\qq1\\\hline 3&1\qq2\qq1\\\hline 4&1\qq3\qq3\qq1\\\hline 5&1\qq4\qq6\qq4\qq1\\\hline 6&1\qq5\qq10\qq10\qq5\qq1\\\hline 7&1\qq6\qq15\qq20\qq15\qq6\qq1\\\hline 8&1\qq7\qq21\qq35\qq35\qq21\qq7\qq1\\\hline 9&1\qq8\qq28\qq56\qq70\qq56\qq28\qq8\qq1\\\hline 10&1\qq9\qq36\qq84\qq126\qq126\qq84\qq36\qq9\qq1\\\hline 11&1\qq10\qq45\qq120\qq210\qq252\qq210\qq120\qq45\qq10\qq1\\ \end{array}

其中第 $i$ 行第 $j$ 个数，表示的是 $(a+1)^{i-1}$ 的 $j-1$ 次项系数。

一些性质¶

我们讨论二项式系数，

\boxed{{n\choose 0},{n\choose 1}.\dots,{n\choose n}}

提示：二项式系数只是组合数，但是提到系数就需要把具体的数字的系数乘进去，比如说 $(3a+2)^2$ 的第一项的二项式系数是 $C(2,0)=1$ ，但是系数是 $3^2\times1=9$ 。

中的单调性，设，

f(n,k)={n\choose k}

则若，

q={f(n,k+1)\over f(n,k)}

考虑化简，

q={f(n,k+1)\over f(n,k)}={n!\over(k+1)!(n-k-1)!}\times{k!(n-k)!\over n!}={n-k\over k+1}

讨论，

函数单增： $q>1\Rightarrow k<\dfrac{n-1}{2}$ ；
函数单减： $q<1\Rightarrow k>\dfrac{n-1}{2}$ 。

据此，我们得出其单增、单减区间为，

\left[0,{n-1\over2}\right] , \left({n-1\over2},n\right]

应用顶、底函数，化简，

\boxed{ \left[0,\left\lfloor{n\over2}\right\rfloor\right] , \left[\left\lceil{n\over2}\right\rceil,n\right] }

因此注意到，

若 $n$ 是偶数，那么存在有唯一的极大值点 $n/2$ ；
若 $n$ 是奇数，那么存在有 $(n+1)/2,(n-1)/2$ 两个极大值点。

一些好玩的题¶

在，

(x+y)(x-y)^5

的展开式中，求下列各式的系数。

我们注意到原式，

(x+y)(x-y)^5=x(x-y)^5+y(x-y)^5

那么如果要求，

x^ny^{6-n}

其实就是前一项的 $x^{n-1}(-y)^{6-n}$ 的系数，

加上后一项 $x^n(-y)^{5-n}$ 的系数，就是

\begin{aligned} (-1)^{6-n}{5\choose6-n}+(-1)^{5-n}{5\choose5-n}\\ =-1^n\left[{5\choose6-n}-{5\choose5-n}\right] \end{aligned}

好玩吧（？

二项式定理做题套路¶

我们知道，

(x_1,x_2,x_3)^n

展开，相当于考虑每一个 $k_1+k_2+k_3=n$ ，

去找，

{n\choose k_1,k_2,k_3}x_1^{k_1}x_2^{k_2}x_3^{k_3}

这么一个贡献，那么我们整理一下，例题：

(x-1+px^2)^6

的展开式中， $x^5$ 项系数最大时的 $p$ 的值。

我们考虑先确定 $x_5$ 的系数，我们知道，可行的能配出来的有，

\begin{aligned} &&(x&-&1&+&p&x^2)^6\\\hline (1)& &1& &3& &2&\\ (2)& &3& &2& &1&\\ (3)& &5& &1& &0& \end{aligned}

下面的表示可以配出 $x^5$ 的系数。

我们把上标看成一共选几个物品，把下面的看成每类物品提供几个。

那么这几个分别对答案的贡献为，

\begin{aligned} (1)&:-60p^2\\ (2)&:60p\\ (3)&:-6 \end{aligned}

合在一起系数为，

-60p^2+60p-6

取最大值时，

p={1\over 2}

这是很直观的。

推导组合性质¶

形式一：

\boxed{(a+1)^n=\sum_{i=0}^n{n\choose i}a^i}

带入 $a=1$ ，

\boxed{\sum_{i=0}^n{n\choose i}=2^n}

带入 $a=2$ ，

\boxed{\sum_{i=0}^n{n\choose i}2^i=3^n}

带入 $a=-1$ ，

\boxed{\sum_{i=0}^n(-1)^i{n\choose i}=[n=0]}

上式，假定 $n\neq0$ ，则，

\sum_{i=0}^n(-1)^i{n\choose i}=0

我们假定 $n$ 是偶数，那么移项，

{n\choose0}+{n\choose2}+\dots+{n\choose n}={n\choose1}+{n\choose 3}+\dots+{n\choose n-1}

且左右相加等于 $2^n$ ，那么左右都等于 $2^{n-1}$ ，即，

{n\choose0}+{n\choose2}+\dots+{n\choose n}=2^{n-1}

{n\choose1}+{n\choose 3}+\dots+{n\choose n-1}=2^{n-1}

对于 $n$ 为正偶数。

类比 $n$ 为正奇数，

{n\choose0}+{n\choose2}+\dots+{n\choose n-1}={n\choose1}+{n\choose 3}+\dots+{n\choose n}

同理，

{n\choose0}+{n\choose2}+\dots+{n\choose n-1}=2^{n-1}

{n\choose1}+{n\choose 3}+\dots+{n\choose n}=2^{n-1}

总结一下，

\boxed{{n\choose0}+{n\choose2}+\dots=2^{n-1}}

\boxed{{n\choose1}+{n\choose 3}+\dots=2^{n-1}}

省略号表示加到小于等于 $n$ 为止。

但是注意到我们规定的后面都为零，因此当成无限加也可以（

进阶内容¶

容斥原理¶

理论¶

容斥原理是一种应用在集合上的较常用的计数方法，其基本思想是：

先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来（容），

然后再把计数时重复计算的数目排斥出去（斥），使得计算的结果既无遗漏又无重复。

容斥原理的核心计数规则可以叙述为：奇加偶减。

例题，将甲乙丙丁四个老师分配到 ABCD 四个班。

要求甲不能在 A，丁不能在 B，求总分配方案数。

用不考虑限制的方案数，减去甲在 A 的，减去丁在 B 的。

注意到甲在 A 且丁在 B，我们是减了两边的，因此加上一次，

4!-2\times3!+2!=24-2\times 6+2=14

完毕！

In general:

\def\abs#1{\left\lvert{#1}\right\rvert} \abs{\bigcup_{i=1}^{n}A_i}=\sum_{S\in[1,n]\wedge\mathbb Z}(-1)^{\abs S-1}\abs{\bigcap_{i\in S}A_i}

简化的形式，

|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|

配合数论知识¶

众所周知， $1\sim n$ 中 $k$ 的倍数有，

\left\lfloor{n\over k}\right\rfloor

好的，你已经会 $1+1=2$ 了，让我们来看一下这个题，

在 $1\sim1000$ 中，有多少个数，既不是 $3$ 的倍数，也不是 $5$ 的倍数。

容易发现，设集合 $A=\#[{\small\sf{是\ 3\ 的倍数}}]$ ， $B=\#[{\small\sf{是\ 5\ 的倍数}}]$ ，则，

\def\floor#1{\left\lfloor{#1}\right\rfloor} |A|=\floor{1000\over3}=333\\[0.5em] |B|=\floor{1000\over5}=200\\[0.5em] |A\cup B|=\floor{1000\over15}=66\\[0.5em] |A\cap B|=|A|+|B|-|A\cup B|=467

那么我们再取一下补集，答案就是 $533$ 。

鸽巢原理¶

此处不讨论第一、第二鸽巢原理。

将 $n+1$ 个物体划分为 $n$ 组，那么有至少一组有两个及以上的物体。

In general:

将 $n$ 个物体划分为 $k$ 组，那么有至少一组有大于等于 $\left \lceil \dfrac{n}{k} \right \rceil$ 个物品。

最差原则：即考虑所有可能情况中，最不利于某件事情发生的情况。也就是最差的情况都能被满足，那么其余所有的情况都比最差的要好，连最差的都能满足，则说明其余所有情况也都能满足，也就是任意情况都能满足。

多重集¶

概念¶

多重集或可重集是集合概念的推广。

在一个集合中，相同的元素只能出现一次，因此只能显示出有或无的属性。
在多重集之中，同一个元素可以出现多次，因此可以显示出元素的个数。

我们可以将其表示为，

\{a_1,a_1,\dots,a_1,a_2,\dots\}

为了简便，下文中我们这么表示，

\{n_1\cdot a_1,n_2\cdot a_2,\dots\}

多重集的排列数¶

多重集 $S=\{n_1\cdot a_1,n_2\cdot a_2,\cdots,n_k\cdot a_k\}$ 的全排列个数为，

{n\choose n_1,n_2,\dots,n_k}={n!\over\prod_{1\le i\le k}n_i}

这个全排列数被称为多重集的排列数，多被称为多重组合数。

注意到，

{n\choose m}={n\choose m,n-m}

但是后面的不常用。

在 $n_1+n_2+\dots=n$ 的情况下，

其直观意义就是，从 $n$ 个中，先选出 $n_1$ 个，再选出 $n_2$ 个，……。

也就是说，我们用弱化的形式，若 $n_1+n_2+n_3=n$ ，

{n\choose n_1,n_2,n_3}={n\choose n_1}{n-n_1\choose n_2}{n-n_1-n_2\choose n_3}

请注意区分，类似

{6\choose 2,2,2}

和，

{6\choose 2,2}

因为其不符合我们上面的和为 $n$ 的要求。

多重集的组合数¶

请注意区分多重组合数（多重集的排列数）和多重集的组合数，他们是完全不同的。

我们类推组合数，以及多重集的排列数，定义如下：

有多重集 $S=\{n_1\cdot a_1,n_2\cdot a_2,\cdots,n_k\cdot a_k\}$ ，那么对于整数 $r$ ，

若 $r$ 满足， $r<n_i,\forall i\in[1,k]$ （注意这个很重要！），

从 $S$ 中选择 $r$ 个元素组成一个多重集的方案数就是多重集的组合数。

这个问题等价于 $x_1+x_2+\dots+x_k=r$ 的非负整数解的数目，可以用插板法解决，答案为，

{r+k-1\choose k-1}

若 $r$ 满足， $r<n,n=\sum_{i=1}^kn_i$ （也就是没有限制了），

则问题可以很容易转化为求解带限制的线性方程，

\forall i\in[1,k],x_i\le n_i,\sum_{i=1}^nx_i=r

好，然而这个过于复杂，我们跳过。

圆排列¶

定义 $n$ 个人全部来围成一圈，所有的排列数记为 $Q(n,n)$ 。

考虑其中已经排好的一圈，从不同位置断开，又变成不同的队列。

所以有，

Q(n,n)={A(n,n)\over n}={n!\over n}=(n-1)!

我们继续类推，即 $Q(n,m)$ 为 $n$ 选 $m$ 个人排成一圈的方案数，

考虑先分组再分配的方案，

Q(n,m)=C(n,m)Q(m,m)={C(n,m)A(m,m)\over m}={A(n,m)\over m}

注意到这里和前面是非常融洽的，我们继续，易得，

Q(n,m)={A(n,m)\over m}={n!\over m(n-m)!}

错位排列¶

错位排列是没有任何元素出现在其有序位置的排列，即，

即，对于 $1\sim n$ 的排列 $P$ ，如果对于所有 $i$ 满足 $P_i\neq i$ ，则称 $P$ 是 $n$ 的错位排列。

例如，三元错位排列有 $\{2,3,1\}$ 和 $\{3,1,2\}$ 。

我们记 $n$ 元错位排列的方案数有 $D_n$ 种，

有前几项（A000166 - OEIS）： $1, 0, 1, 2, 9, 44, 265$ 。

以下是其常用性质，有封闭形式，推导略，

D_n=n!\sum_{k=0}^n{(-1)^k\over k!}

有递推式，

D_n=(n-1)(D_{n-1}+D_{n-2})

这个是经典形式，一个不严谨的证明：

假定第 $n$ 个先放在 $n$ 位置，
若前面的所有已经错位，那么随便找一个，和 $n$ 交换即可满足要求，方案数 $(n-1)D_{n-1}$ ；
若前面的只剩一个没有错位，那么和这个交换，即可满足条件，方案数 $(n-1)D_{n-2}$ ；
总方案数： $D_n=(n-1)(D_{n-1}+D_{n-2})$ 。
可以证明，不存在其他在一步内的构造方案。

还有一些惊人观察力的性质，

设 $P_n$ 表示所有排列中，为错位排列的概率，即，

P_n={D_n\over A(n,n)}={D_n\over n!}

有性质，

\lim_{n\to\infty}P_n={1\over e}

或者也可以表述为，

P=\lim_{n\to\infty}{D_n\over n!}={1\over e}

由此推知，

D_n=\left\lfloor{n!\over e}\right\rfloor

这一个近似求解。

卡特兰数¶

概念¶

卡特兰数可以表示一类组合问题，

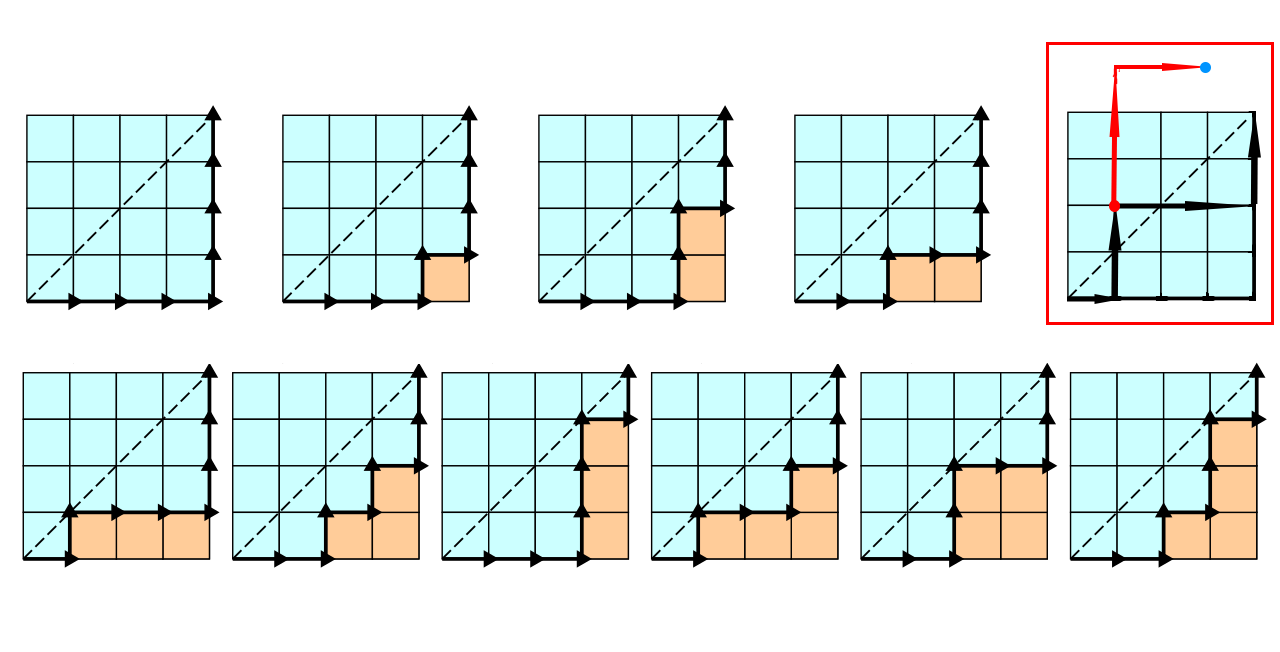
其情景有，

如上图，从左下走到右上，不穿过对角线的方案数；
有 $n$ 个元素，编号 $1\sim n$ ，出入栈的方案数；

推导¶

在上述图像中，容易知道，不考虑限制的方案数为，

{2n\choose n}

种，表示 $2n$ 步中选择 $n$ 步表示往上走。

考虑不合法情况（右上角），容易发现我们把图像从第一次穿越对角线开始翻折，

一定会最终落在终点的左上角位置，因此，不合法方案数为，

{2n\choose n+1}

总方案数为，

\boxed{C_n={2n\choose n}-{2n\choose n+1}}

一个经典公式，考虑继续推导，

\begin{aligned} C_n&={2n\choose n}-{2n\choose n+1}\\ &={(2n)!\over n!n!}-{(2n)!\over (n+1)!(n-1)!}\\ &={(2n)!\over n!n!}-{(2n)!\over n!n!}\cdot{n\over n+1}\\ &={1\over n+1}\cdot{(2n)!\over n!n!}\\ &={1\over n+1}{2n\choose n} \end{aligned}

即经典公式，

\boxed{C_n={1\over n+1}{2n\choose n}}

还有不常用公式，

C_n=C_{n-1}\cdot{4n-2\over n+1}

有卡特兰数列（A000108 - OEIS），

1, 1, 2, 5, 14, 42, 132,\dots

Lucas 定理¶

对于素数 $p$ ，

{n\choose m}\equiv{n\bmod p\choose m\bmod p}\cdot{\lfloor n/p\rfloor\choose\lfloor m/p\rfloor}\pmod p

或用更不直观的表达（？

对于 $n,m$ 在 $p$ 进制下有表示，

\begin{cases} n&=a_0+a_1p+\dots+a_kp^k\\ m&=b_0+b_0p+\dots+b_kp^k \end{cases}

那么，

{n\choose m}=\prod_{i=0}^k{a_i\choose b_i}

可以用于推导一些模意义下的性质。

广义二项式定理¶

对于实数 $n$ ，

(a+b)^n=\sum_i{n^{\underline k}\over k!}x^{n-k}y^k

似乎用处不大。

常见解题技巧和模型¶

我会在一个单独的技巧里面穿插一些与其不相关的。

目的是让你知道，模型不是全都直接套的，而是看情况。

（有的时候其实枚举更快（？

特殊优先策略¶

情景就是你事情最多我就特殊处理你。

不一定是优先，也可以是后置处理（插空法）。

例题一¶

六个人排队，甲不在排头。

Solution 1：考虑甲只有 $5$ 种方法，剩下五个人排列插入即可。

5\times A(5,5)=600

Solution 2：插空法，五个人排好后，甲插入除了开头的一个空。

A(5,5)\times C(5,1)=600

例题二¶

六个人排队，甲不在队头，丁（？）不在队尾。

直接插空法，我们先放甲，

A(4,4)\times C(4,1)\times C(5,1)=480

但是还有一种情况，甲先选了队头，但是丁插她前面了（？

A(4,4)=24

总答案为，

280+24=504

例题三¶

六个人排队，甲不在队头，丁不在队尾，且甲丁 xql 不相邻（？。

我们这个做法的优势体现了。

我们还是插空法，先放甲，注意此时出问题了。

我们再分讨，若甲选了队尾，

A(4,4)\times C(4,1)=96

否则，甲没选队尾，

A(4,4)\times C(3,1)\times C(3,1)=216

那么总有。

96+216=312

种。

等效替代策略¶

当我们需要计算一些带特殊条件的方案数时，可以用一些等价替代的方法。

具体来讲，我们构造一个双射，将每一种原问题的方案映射为新问题的一种方案，并使答案更容易计算。

常用的有捆绑法、插空法、隔板法等。

捆绑法¶

有七个人站队拍照，甲和乙要求相邻，丙和丁要求相邻，求方案数。

注意到我们把甲和乙替换为他们的儿子，丙和丁替换为他们的女儿，那么我们将这 $5$ 个新人排列，

A_5^5=5\times4\times3\times2\times1=120

然后把儿子替换为甲和乙，把女儿替换为丙和丁，那么这两个小组分别再排列，总答案为，

A^5_5\times A^2_2\times A_2^2=480

种，那么这就是捆绑法。

插空法¶

有七个人拍照，由于甲和乙关系很好，他们要求不相邻，求方案数。

注意到我们先不管甲和乙，排列数，

A_5^5=5\times4\times3\times2\times1=120

然后把甲和乙插进这 $5$ 个人形成的 $6$ 个空中，总答案为，

A_5^5\times A_2^2=240

种，那么这就是插空法。

例题：现在五个人顺序已确定，插入两人，共有几种方案。

若相邻，捆绑插空， $C_6^1=6$ 种．
不相邻，上文已述， $240$ 种．

那么，显然这两个没有交集，我们直接加一起，总答案为 $246$ 种。

插板法¶

插板法是用于求一类给相同元素分组的方案数的一种技巧。

同时，也可以用于求一类线性不定方程的解（正整数解、非负整数解）的组数。

\mathsf{\bold{情况一：正整数解}}

求：

x_1+x_2+\dots+x_k=n

的正整数解的解的组数。

情景：
把 $n$ 个小球分成 $k$ 个不同的组，每组个数不为零，求情况数。

考虑拿 $k-1$ 块板子插入到 $n$ 个元素两两形成的 $n-1$ 个空里面，因此答案就是，

\boxed{{n-1\choose k-1}}

\mathsf{\bold{情况二：非负整数解}}

求：

x_1+x_2+\dots+x_k=n

的非负整数解的解的组数。

情景：
把 $n$ 个小球分成 $k$ 个不同的组，每组个数可以为零，求情况数。

我们还是用 $k-1$ 个板子来分成 $k$ 组，但是可以为零。

不妨令 $y_i=x_i+1$ ，那么原方程，

y_1+y_2+\dots+y_k=n+k

注意到 $y_i$ 就一定是正整数了，答案为，

\boxed{{n+k-1\choose k-1}}

情景就是我们借给他 $k$ 个元素，那么选完之后再删掉这几个，就行了。

\mathsf{\bold{情况三：不等式}}

求：

x_1+x_2+\dots+x_k\le n

的非负整数解的解的组数。

注意到原式等价于，再加上一个非负整数，

x_1+x_2+\dots+x_k+x_{k+1}=n

于是，答案为，

{n+k\choose k}

\mathsf{\bold{例题一：简单应用}}

有 $10$ 球分给 $4$ 人，甲必须有，方案数。

相当于，

x_1+x_2+x_3+x_4=10

其中 $x_1\ge1$ ，另 $y_1=x_1-1$ ，则，

y_1+x_2+x_3+x_4=9

对于非负整数解个数，即，

{12\choose 3}={12\times11\times10\over3\times2\times1}=220

\mathsf{\bold{例题二：配合容斥原理}}

这一部分配合容斥是经典套路了。

题目， $24$ 个小球分给 $3$ 个盒子，要求每个盒子至少一个且互不相同，求方案数。

容易发现，记，

a+b+c=24

答案即为，

\def\card#1{\#[#1]} \card{}-\card{a=b}-\card{a=c}-\card{b=c}+2\times\card{a=b=c}\\

注：为了简写，两两不等的省略。我们分别来看，

\#[]={23\choose 2}=253\\

考虑 $\#[x_i=x_j]$ 是多少。

容易发现，即，

2t+x=24

因为都是正整数，因此，

t\in(0,12)

共有 $11$ 种，因此，

\def\card#1{\#[#1]} \card{a=b}=\card{b=c}=\card{a=c}=11\\

而，

\#[a=b=c]=1

是显然的；因此，答案，

253-33+2=222

先整体后局部策略¶

先把一个集合的位置确定，再确定集合内的。

如果是先确定集合内的，再确定集合整体位置，也可以视为插空法的一般形式。

例题：五个男生和五个女生拍照，要求同性相邻（不是同性恋）的方案数。

首先，我们先排男生和女生的次序 $A(2,2)$ 。

然后男生内部和女生内部分别有 $A(5,5)$ 的方案。

总答案为 $A(2,2)\times A(5,5)\times A(5,5)$ 。

正难则反策略¶

经典的。

例题：班里 $50$ 人选 $5$ 人出去玩，要求正副班长和团支部书记至少一人在内，方案数。

首先我们正着做肯定是枚举那个人在里面，然后随便选。

但是反着做也很简单，我们考虑没有限制的方案数，

{50\choose 5}

但是有一些是不符合条件的，即三个人都不在，那么这个有多少种方案？

{47\choose 5}

那么减掉，

{50\choose 5}-{47\choose 5}

就是总方案数。

成套思想¶

若展开式，

(3x-1)^8=a_8x^8+a_7x^7+\dots+a_1x+a_0

求 $a_8+a_6+a_4+a_2+a_0$ 。

收到上面的启发，我们考虑设，

A=a_8+a_6+a_4+a_2+a_0

B=a_7+a_5+a_3+a_1

我们考虑求出，

\begin{cases} A+B=\\ A-B= \end{cases}

就可以了。

下面是一些技巧。

我们知道系数 $a_0\sim a_8$ 都是常数（与 $x$ 无关）且一定对所有有意义的 $x$ 成立。

那么这一位置我们可以随意带入 $x$ 以获得这些数的确切关系，比如，

带入 $x=1$ ，

2^8=a_8+a_7+\dots+a_0

即，

A+B=256

带入 $x=-1$ ，

4^8=a_8-a_7+\dots+a_0

即，

A-B=2^{16}=65536

那么，易得，

\begin{cases} A&=32 896\\ B&=−32 640 \end{cases}

证明整除问题¶

例题一

\begin{aligned} (n+1)^n-1&={n\choose1}n+{n\choose2}n^2+\dots+{n\choose n}n^n\\ &=n^2+{n\choose2}n^2+\dots+{n\choose n}n^n \end{aligned}

可以被 $n^2$ 整除。

例题二

我们尝试一些抽象的方法，

99^{10}-1\equiv(-1)^{10}-1\equiv1^5-1\equiv0\pmod{100}

好玩（

例题三

我们尝试一些可爱的方法，

55^{55}+9\equiv7^{55}+1\equiv(-1)^{55}+1\equiv0\pmod8

好玩（

啊这跑题了（二项式定理哭哭）。

其实一个比较直观的理解方式，就是下面写成待遇出发，

a=qm+r,r\in[0,m)

的形式，那么二项式定理，后面所有项都有模数的倍数，消去即得。

伯努利不等式¶

简单形式，对于实数 $x\ge-1$ ，

若 $n\ge1$ ，则 $(1+x)^n\ge1+nx$ ；
若 $0\le n\le1$ ，则 $(1+x)^n\le1+nx$ 。

可以看到等号成立当且仅当 $n = 0,1$ 或 $x = 0$ 时。

二项式定理展开丢掉后面的项即可。

倍缩法和可重策略¶

例题： $7$ 个人排队，甲乙丙顺序一定的情况下的方案数。

也可以鉴定为，甲乙丙顺序不重要的方案数。

我们可以用 $7$ 个人排列的方案数，除去甲乙丙的方案数。

意义就是，排列完 $A(7,7)$ ，每 $A(3,3)$ 个就可以分为一组，

这一组内，除甲乙丙外顺序相同。

对于这若干个组，除去这个 $A(3,3)$ 就是答案，

{A(7,7)\over A(3,3)}=A(7,4)=7\times6\times5\times4=840

可重集会具体讲。

多排问题直排策略¶

六个人照相排队，分两排，每排三人，共有几种排队方式。

Solution 1：先选三人，排列；剩下三人排列。

\begin{aligned} C(6,3)A(3,3)A(3,3)\\ ={6\times5\times4\over3\times2\times1}\times3\times2\times1\times3\times2\times1\\ =6\times5\times4\times3\times2\times1=720 \end{aligned}

Solution 2：注意到等价于六个人排列，后三个自动补到后一排。

A(6,6)=6\times5\times4\times3\times2\times1=720

总结：这种分组但是每组有区别的，可以合在一起考虑。

模型和穷举策略¶

模型，即将问题归纳为多个已有模型的组合。

穷举，即枚举，一般是结合先分组再分配、特殊优先处理。

模型一：排数问题¶

例题：用 $0\sim9$ 可以排成多少个，

不同的三位数：

Sol1： $999-100+1=900$ ．
Sol2： $9\times10\times10=900$ ，即第一位除了 $0$ ，后面随意。

没有重复数字的三位数：

Sol： $9\times9\times8=648$ ．

没有重复数字的三位奇／偶数：

奇数：最后一位 $1,3,5,7,9$ ．
共有 $5\times8\times8=320$ 种数字．

偶数：最后一位 $0,2,4,6,8$ ．
若是 $0$ ，有 $9\times8=72$ 种数字．
否则 $4\times8\times8=256$ 种数字．
共有 $72+256=328$ 种数字．

加强：没有重复数字的 $>300$ 的三位偶数：

Sol：正难则反，用 $328$ 减去小于等于的。

第一位 $1$ ： $5\times8=40$ ；
第一位 $2$ ： $4\times8=32$ ．

答案： $328-40-32=256$ ．

模型二：球盒模型¶

注：因为作者懒得改下面不严谨的地方了，没有说明默认不考虑无解的情况（方案数为零）。

题型一：平均分配¶

九个小球分给三个人，求方案数。

若人和球都不同。

第一个人选 $3$ 个，第二个人从剩下的 $6$ 中中选……

{9\choose3}{6\choose3}{3\choose3}

也记为，

{9\choose3,3,3}

若人相同，球不同。

注意到相当于人球不同中，每 $A(3,3)$ 个对应一个有效情况。

因此，答案为，

{9\choose3,3,3}\bigg/\begin{matrix}\\A(3,3)\end{matrix}

若人和球都相同。

那么只有一种情况就是每人三个球呗。

若人不同，球相同。

那么只有一种情况就是每人三个球呗（？

题型二：不完全平均分配¶

七球三人，一人 $3$ 球，其他人 $2$ 球，求方案数。

若人和球都不同。

我们随便类比，答案为，

{7\choose3,2,2}

注意到一定不存在重复。

若人相同，球不同。

注意到只有大小相同的集合会重复。

具体的，若一个人选了集合 $A$ ，另一个人选了 $B$ 。

那么，当且仅当 $|A|=|B|$ 时，交换 $A,B$ 才是等价的。

也就是说我们除去这个数字的大小的 $|A|!$ 才是最终答案。

容易发现我们上一个模型中，除去的 $A(3,3)$ 本质也是一样的。

也就是说上一个模型本质是这个模型的一个子集。

说了这么半天写一下公式把，

{7\choose3,2,2}\bigg/\begin{matrix}\\A(2,2)\end{matrix}

其他：显然为 $1$ 哦。

题型三：完全不平均分配¶

本质还是上面的子集，但是注意到 $A(1,1)=1$ 罢了。

题型四：十二重计数法选讲¶

有 $n$ 个球，放到 $m$ 个盒子中，求方案数。

I. 球不同，盒子不同，无其他限制

每个球可以放到不同的 $m$ 个盒子中，因此答案为，

m^n

II. 球不同，盒子不同，每个盒子至多装一个球

显然若 $n>m$ 则无解。

否则，注意到相当于在 $m$ 个盒子中选择 $n$ 个来放球，

C(m,n)P(n,n)=P(m,n)=m^{\underline n}

先分组再分配策略，也可以理解按照顺序每个球可行位置递减。

III. 球不同，盒子不同，每个盒子至少装一个球

我们强令 $i$ 个盒子为空，其他盒子无限制。

那么我们容斥，

\sum_{i=0}^m(-1)^i{m\choose i}(m-i)^n

就是答案。

具体的，减去有空的，但是重复了，因此容斥。

IV. 球不同，盒子相同，无其他限制

第二类斯特林数 · 行，本文不讲。

V. 球不同，盒子相同，每个盒子至多装一个球

注意到答案即为，

[n\le m]

用艾佛森括号表示。

VI. 球不同，盒子相同，每个盒子至少装一个球

第二类斯特林数板子题，本文不讲。

VII. 球相同，盒子不相同，无其他限制

插板法，

{n+m-1\choose m-1}

即为答案。

VIII. 球相同，盒子不相同，每个盒子至多装一个球

我们要选出来 $n$ 个盒子装球，其他的不装球，

{m\choose n}

即为答案。

IX. 球相同，盒子不相同，每个盒子至少装一个球

插板法，

{n-1\choose m-1}

即为答案。

X. 球相同，盒子相同，无其他限制

划分数问题，过于抽象，不讲。

XI. 球相同，盒子相同，每个盒子至多装一个球

和 V. 一样，答案为，

[n\le m]

用艾佛森括号表示。

XII. 球相同，盒子相同，每个盒子至少装一个球

同为划分数，不讲。

组合数大型运算推导¶

下面默认 $n$ 是任意自然数，一般 $k\le n$ 。

例题一，证明：

\sum_{i=0}^k(-1)^i{n\choose i}=(-1)^k{n-1\choose k}

对于 $n<k$ ，且 $n,k$ 都是正整数。

很多题解使用了数学归纳法，这里用了一种比较好的方法：扰动法。

考虑证明，

\begin{aligned} \sum_{i=0}^k(-1)^i{n\choose i}+(-1)^{k+1}{n\choose k+1}&=1+\sum_{i=0}^k(-1)^{i+1}{n\choose i+1}\\ &=1-\sum_{i=0}^k(-1)^i{n\choose i+1} \end{aligned}

我们似乎没有思路了，但是注意到，

{n\choose i}+{n\choose i+1}={n+1\choose i+1}

于是，我们移项，

\begin{aligned} \sum_{i=0}^k(-1)^i{n+1\choose i+1}&=1-(-1)^{k+1}{n\choose k+1}\\ \sum_{i=1}^{k+1}(-1)^{i-1}{n+1\choose i}&=1-(-1)^{k+1}{n\choose k+1}\\ \sum_{i=1}^{k+1}(-1)^i{n+1\choose i}&=-1+(-1)^{k+1}{n\choose k+1}\\ \sum_{i=0}^{k+1}(-1)^i{n+1\choose i}&=(-1)^{k+1}{n\choose k+1}\\ \end{aligned}

我们令 $n\gets n-1,k\gets k-1$ ，得，

\begin{aligned} \sum_{i=0}^k(-1)^i{n\choose i}&=(-1)^k{n-1\choose k}\\ \end{aligned}

得证。

例题二，证明：

\sum_{k=0}^n{1\over k+1}{n\choose k}={1\over n+1}(2^{n+1}-1)

我们考虑展开里面，

{1\over k+1}{n\choose k}={n!\over(k+1)!(n-k)!}={1\over n+1}\cdot{n+1\choose k+1}

那么我们推导，

\sum_{k=0}^n{1\over k+1}{n\choose k}={1\over n+1}\sum_{k=0}^n{n+1\choose k+1}

我们另 $t=n+1$ ，右侧变为，

{1\over t}\sum_{k=1}^t{t\choose k}={1\over t}(2^t-1)

重新放回去，即得，

\sum_{k=0}^n{1\over k+1}{n\choose k}={1\over n+1}(2^{n+1}-1)

例题三，证明：

\sum_{k=0}^n{(-1)^k\over k+1}{n\choose k}={1\over n+1}

我们根据上一题的结论，

\sum_{k=0}^n{(-1)^k\over k+1}{n\choose k}={1\over n+1}\sum_{k=0}^n(-1)^k{n+1\choose k+1}

继续另 $t=n+1$ ，右侧变为，

{1\over t}\sum_{k=1}^t(-1)^{k-1}{t\choose k}={1\over t}\left[\sum_{k=0}^t(-1)^{k-1}{t\choose k}\right]+{1\over t}

根据二项式定理，

(a+1)^t=\sum_{k=0}^ta^k{t\choose k}

带入 $a=-1$ ，得，

\sum_{k=0}^t(-1)^k{t\choose k}=[t=0]

我们知道 $t>n\ge0$ ，即右侧一定为 $0$ ，即，

\sum_{k=0}^n{(-1)^k\over k+1}{n\choose k}={1\over n+1}

本页面最近更新：2025/3/2 21:05:16，更新历史。
编辑页面：在 GitHub 上编辑此页！
本页面贡献者：RainPPR。